Tempos atrás, num post do Meeple Divino na Ludopedia, vi alguns comentários interessados sobre a contagem de peças em Carcassonne. No post, o Rodrigo Deus havia apresentado uma resenha simples sobre o jogo e, nos comentários, alguns usuários (inclusive eu) comentavam sobre as possibilidades estratégicas no clássico de Klaus-Jürgen Wrede. Até que o usuário Moita1980 ressaltou que o jogo só poderia ser jogado de modo muito estratégico com a contagem de peças. E, nesse ponto, foi questionado: “contagem de peças, como assim?!” Então dei um exemplo bem simples de como a contagem de peças poderia ser usada estrategicamente em Carcassonne, e, à convite do amigo Rodrigo Deus, vou trazendo um pouquinho mais sobre isso e outras questões estratégicas de Carcassonne aqui para o blog.
Então, para começar, vamos pelas peças existentes em Carcassonne!
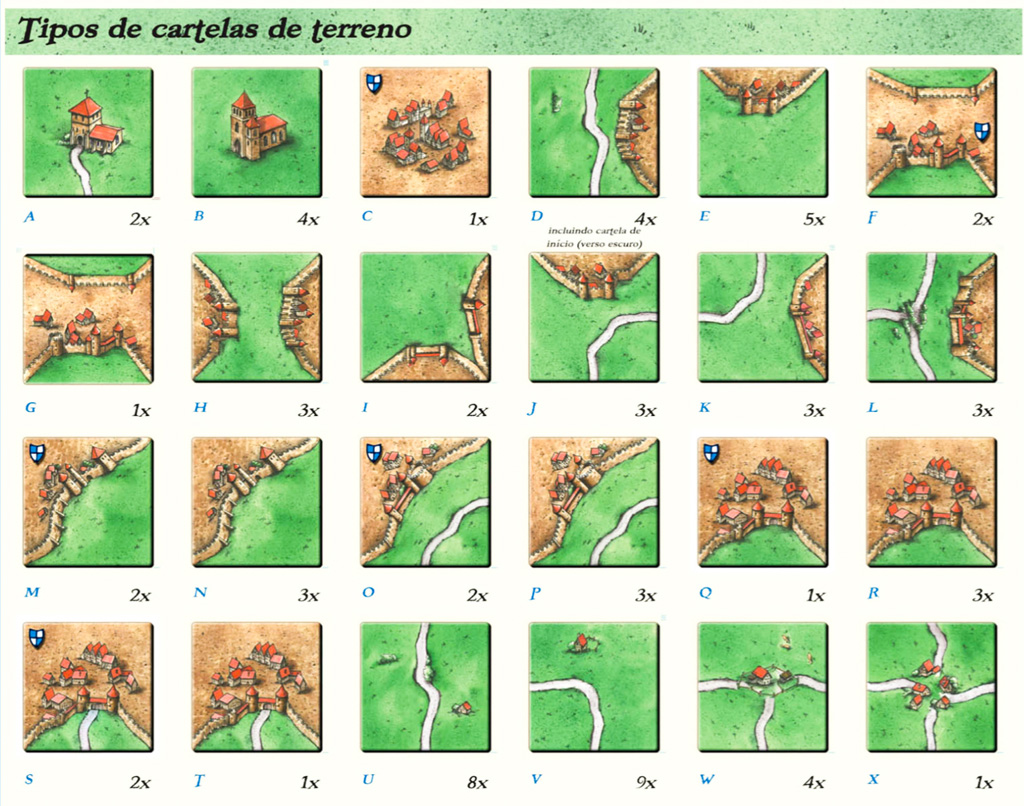
Infelizmente, o manual da atual edição da Devir não trouxe o quadro de todas as peças do jogo base — como existia no manual da Grow. Mas, de qualquer forma, as peças são as mesmas e, desde a primeira versão do jogo, pouca coisa mudou em relação às regras. Uma das diferenças da versão atual para outras versões é que agora os castelos compostos por apenas dois tiles valem 4 pontos, e não 2, como em versões mais antigas.
As peças de castelo
Ao todo, são 13 os tipos de peças com castelo existentes. Conhecer as peças de castelo existentes é muito importante para bloquear jogadas do adversário baseando-se na quantidade de peças ainda disponíveis no estoque de compras. Além disso, com a contagem é possível se proteger melhor de possíveis bloqueios planejados pelo oponente no decorrer do jogo!
1) Exemplo de contagem para bloqueio contra o oponente:
Digamos que o jogador azul tenha em mãos a peça deslocada (curva simples) e pretenda utilizá-la para bloquear os dois meeples (seguidores) do adversário vermelho. Ele teria, então, duas opções para o encaixe da peça:
Opção A
Opção B

Qual seria a melhor opção para reduzir as possibilidades do jogador vermelho? Para a opção A, seria necessária a peça de castelo com rua reta em cima para a liberação dos meeples. Para a opção B, a peça necessária seria a de castelo com trevo. Podemos contar 3 peças de castelo com reta e 3 também do tipo castelo com trevo presentes no tabuleiro montado. Considerando que no jogo existem apenas 3 peças de castelo com trevo contra 4 de castelo com reta, existe, no monte de compras, 1 peça para a opção A e 0 (nenhuma) peça para a opção B. Portanto, para travar definitivamente os dois meeples do jogador vermelho, a opção B seria a melhor decisão.
2) Exemplo de contagem para defesa:
Para esse segundo exemplo, vamos imaginar que o jogador vermelho pretende se defender/aumentar suas possibilidades de contar pontos e liberar seus dois meeples alocados. Vamos utilizar, novamente, duas opções diretas para a colocação da peça.
Opção A

Opção B
Para a opção A, a peça necessária para a liberação dos meeples é a peça de letra O/P que pode ser encontrada na primeira imagem do post. Para a opção B, a peça de letra L seria a opção útil (castelo com trevo). Ao contar as peças, a opção A se mostra eficiente, já que ainda existem 4 peças do tipo na pilha de compras. Para a opção B, não existem mais peças disponíveis para comprar.
As peças de estrada
As peças com estrada são muitas, e, por isso, podemos dividir em peças COM RETA, peças COM CURVA e peças de TREVO.
Saber quais e quantas são as peças com estrada é útil para compartilhar/roubar estradas do adversário, bloquear estradas, etc.
Vou utilizar um exemplo similar aos anteriores para exemplificar, mais uma vez, a utilização da contagem de peças — agora, com a colocação de estradas para bloquear estradas.
Para bloquear o meeple vermelho temos, mais uma vez, duas opções.
Opção A, colocando a curva virada para dentro, na direção do trevo abaixo do monastério. Ou opção B, jogando a curva para fora, do lado oposto. Mentalizou? Pois então. Para bloquear o adversário, a melhor jogada para o azul seria a opção A.
Podemos também pensar no mesmo exemplo para a defesa do meeple vermelho. Se a jogada fosse realizada pelo jogador vermelho, e este quisesse utilizar a peça para a defesa do meeple, a opção B seria eficiente. Pois, com a contagem temos: NENHUMA peça disponível para a opção A (trevo de quatro pontas) versus 3 peças ainda disponíveis para a opção B (trevo de 3 pontas).
As peças de monastério
São apenas DOIS os tipos de monastério no jogo base:

Assim como para os outros tipos de peça, saber a quantidade de monastérios também aumenta as possibilidades de montar estratégias de acordo com o número de peças existentes no estoque.
+ Por que o campeonato nacional/mundial de Carcassonne é disputado em mesas exclusivamente de dois jogadores?
A contagem de peças é um aspecto fundamental para as estratégicas utilizadas em Carcassonne. Em dois jogadores é possível utilizar a contagem de modo mais controlado, já que as possibilidades podem ser calculadas para apenas 2 lados. Quanto mais pessoas em jogo, menos controles temos sobre as possibilidades em pegar algumas peça específica. Além disso, a quantidade reduzida de ações — já que a quantidade de tiles é a mesma para 2, 3, 4 ou 5 jogadores — reduz, e muito, as jogadas de bloqueio. Usar uma ação para bloquear o adversário ao invés de pontuar, numa partida de 2 jogadores, é mais eficiente e comum do que em partidas com mais pessoas. Sem as estratégicas de bloqueio, defesa e outros, Carcassonne acaba se tornando um jogo com muito mais sorte envolvida que depende muito dos riscos não-calculados de pegar essa ou aquela peça.










